library(Matrix)
library(sandwich)
mydata <- read.csv(http://www.ats.ucla.edu/stat/data/binary.csv)
mylogit <- glm(admit ~ gre + gpa, data = mydata, family = "binomial")
X <- as.matrix(cbind(1, mydata[,c('gre','gpa')]))
n <- nrow(X)
pi<-mylogit$fit
w<-pi*(1-pi)
v<-Diagonal(n, x = w)
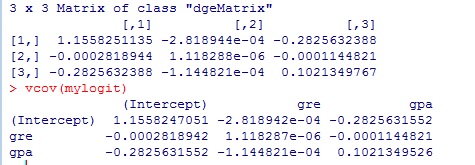
var_b<-solve(t(X)%*%v%*%X)
var_b
vcov(mylogit)
Every time I think I know what's going on, suddenly there's another layer of complications.
2015年8月16日星期日
2015年8月7日星期五
Understanding and correcting complete or quasi-complete separation problems
This is a common problem with logistic models. Unlike in ordinary least-squares regression for modeling a normally distributed response, when a logistic model perfectly or nearly perfectly predicts the response (that is, separates the response levels), unique maximum likelihood estimates do not exist. Some model parameters are actually infinite. This is a common result of the data being sparse, meaning that not all response levels are observed in each of the predictor settings, which often happens with small data sets or when the event is rare. See "Existence of Maximum Likelihood Estimates" in the Details section of the LOGISTIC documentation.
When the separation condition is detected, the procedure terminates the maximum likelihood iteration process and reports the results at the last iteration. The resulting model is often quite good at classifying observations and might be usable for this purpose, but inferences about the parameters based on Wald chi-square statistics should be avoided. For details about the stopping rule, see the "Existence of Maximum Likelihood Estimates" section of the LOGISTIC documentation and the So reference.
One possible solution to the separation problem is to make the model fit less perfectly by reducing the number of variables or effects in the model, categorizing continuous variables, or merging categories of categorical (CLASS) variables. It is often difficult to know exactly which variables cause the separation, but variables that exhibit large parameter estimates or standard errors are likely candidates.
When developing a model, it can be very helpful to use forward or stepwise (not backward) selection via the SELECTION= option in the MODEL statement. These methods build a model that might avoid separation, or if separation occurs in a model fit at a particular step, you might consider using the model successfully fit at the previous step.
Valid tests of model effects can be obtained by using likelihood ratio (LR) tests rather than the Wald tests that are presented by PROC LOGISTIC. For models that do not involve survey data, the easiest way to do this is to fit the model in PROC GENMOD (use the DIST=BINOMIAL option in the MODEL statement) and use the TYPE3 option or the CONTRAST statement to obtain LR tests.
Because separation often happens with small data sets, another possible solution is to use exact logistic regression, which is available via the EXACT statement in PROC LOGISTIC. However, exact methods are very computationally intensive and can take great amounts of time and/or memory even for moderate sized problems. A penalized likelihood method by Firth can often converge to a solution even though a unique solution by maximum likelihood does not exist in separation cases. Firth's method is available, beginning in SAS 9.2, by specifying the FIRTH option in the MODEL statement.
If interest lies exclusively in testing the association of one predictor with the response while adjusting for the effects of the other predictors, then you could use the CMH option in PROC FREQ. All predictors other than the one of interest are used as stratifying variables. Since no model is fit by PROC FREQ, the problem of infinite parameters caused by separation is not an issue. For example, consider the final model involving Sex, Age, and Treatment in the example titled "Logistic Modeling with Categorical Predictors" in the LOGISTIC documentation. The following statements test the association of Treatment with the response, Pain, while adjusting for Sex and Age. The NOPRINT option is used to avoid displaying the large multi-way table. The CMH option computes the test. Since Treatment is an unordered categorical variable with three levels, the second CMH statistic labeled "Row Mean Scores Differ" is an appropriate test.
Usage Note 22599: Understanding and correcting complete or quasi-complete separation problems
When the separation condition is detected, the procedure terminates the maximum likelihood iteration process and reports the results at the last iteration. The resulting model is often quite good at classifying observations and might be usable for this purpose, but inferences about the parameters based on Wald chi-square statistics should be avoided. For details about the stopping rule, see the "Existence of Maximum Likelihood Estimates" section of the LOGISTIC documentation and the So reference.
One possible solution to the separation problem is to make the model fit less perfectly by reducing the number of variables or effects in the model, categorizing continuous variables, or merging categories of categorical (CLASS) variables. It is often difficult to know exactly which variables cause the separation, but variables that exhibit large parameter estimates or standard errors are likely candidates.
When developing a model, it can be very helpful to use forward or stepwise (not backward) selection via the SELECTION= option in the MODEL statement. These methods build a model that might avoid separation, or if separation occurs in a model fit at a particular step, you might consider using the model successfully fit at the previous step.
Valid tests of model effects can be obtained by using likelihood ratio (LR) tests rather than the Wald tests that are presented by PROC LOGISTIC. For models that do not involve survey data, the easiest way to do this is to fit the model in PROC GENMOD (use the DIST=BINOMIAL option in the MODEL statement) and use the TYPE3 option or the CONTRAST statement to obtain LR tests.
Because separation often happens with small data sets, another possible solution is to use exact logistic regression, which is available via the EXACT statement in PROC LOGISTIC. However, exact methods are very computationally intensive and can take great amounts of time and/or memory even for moderate sized problems. A penalized likelihood method by Firth can often converge to a solution even though a unique solution by maximum likelihood does not exist in separation cases. Firth's method is available, beginning in SAS 9.2, by specifying the FIRTH option in the MODEL statement.
If interest lies exclusively in testing the association of one predictor with the response while adjusting for the effects of the other predictors, then you could use the CMH option in PROC FREQ. All predictors other than the one of interest are used as stratifying variables. Since no model is fit by PROC FREQ, the problem of infinite parameters caused by separation is not an issue. For example, consider the final model involving Sex, Age, and Treatment in the example titled "Logistic Modeling with Categorical Predictors" in the LOGISTIC documentation. The following statements test the association of Treatment with the response, Pain, while adjusting for Sex and Age. The NOPRINT option is used to avoid displaying the large multi-way table. The CMH option computes the test. Since Treatment is an unordered categorical variable with three levels, the second CMH statistic labeled "Row Mean Scores Differ" is an appropriate test.
proc freq data=Neuralgia;
table Sex * Age * Treatment * Pain / noprint cmh;
run;
The resulting p-value (0.0040) closely matches the p-value of the Treatment Type3 test from the logistic model (0.0018) Usage Note 22599: Understanding and correcting complete or quasi-complete separation problems
2015年6月30日星期二
2015年6月27日星期六
EM alogrithm for mixed Normal distribtuion
Data are from Robert Hogg Exercise 6.6.8
library(car)
x<-c(119.0,96.0,146.2,138.6,143.4,98.2,124.5,114.1,136.2,136.4,
184.8,79.8,151.9,114.2,145.7,95.9,97.3,136.4,109.2,103.2)
densityPlot(x)
p_0<-0.6
u1_0<-105
u2_0<-130
sigma1_0<-15
sigma2_0<-25
p<-c()
pi<-c()
u1<-c()
u2<-c()
sigma1_2<-c()
sigma2_2<-c()
s<-c()
s1<-c()
diff<-c()
j<-1 #this is imporant
s<-c(p_0,u1_0,u2_0,sigma1_0^2,sigma2_0^2) #initial guess of p,u1,u2,sigma1, sigma2
p_i_0<-p_0*dnorm(x,u2_0,sigma2_0)/((1-p_0)*dnorm(x,u1_0,sigma1_0)+p_0*dnorm(x,u2_0,sigma2_0))
p[j]<-mean(p_i_0)
u1[j]<-sum((1-p_i_0)*x)/sum(1-p_i_0)
u2[j]<-sum(p_i_0*x)/sum(p_i_0)
sigma1_2[j]<-sum((1-p_i_0)*(x-u1_0)^2)/sum(1-p_i_0)
sigma2_2[j]<-sum(p_i_0*(x-u2_0)^2)/sum(p_i_0)
s1<-c(p[j],u1[j],u2[j],sigma1_2[j],sigma2_2[j])
for(i in 1:5){
diff[i]<-abs(s1[i]-s[i])
}
for(i in 1:5){ #in fact we don't need this, we can mainly focus on p
while(diff[i]>0.000001){
s<-c(p[j],u1[j],u2[j],sigma1_2[j],sigma2_2[j])
p_i<-p[j]*dnorm(x,u2[j],(sigma2_2[j])^0.5)/((1-p[j])*dnorm(x,u1[j],sigma1_2[j]^0.5)+p[j]*dnorm(x,u2[j],sigma2_2[j]^0.5))
#p_i will be updated by p,u1,u2,sigma1 and sigma2
u1[j+1]<-sum((1-p_i)*x)/sum(1-p_i)
u2[j+1]<-sum(p_i*x)/sum(p_i)
sigma1_2[j+1]<-sum((1-p_i)*(x-u1[j+1])^2)/sum(1-p_i)
sigma2_2[j+1]<-sum(p_i*(x-u2[j+1])^2)/sum(p_i)
p[j+1]<-mean(p_i)
s1<-c(p[j+1],u1[j+1],u2[j+1],sigma1_2[j+1],sigma2_2[j+1])
diff[i]<-abs(s1[i]-s[i])
j=j+1
}
}
#results:
After 301 iterations all parameters are within 0.00000 accuracy
For p:
[1] 0.6446007 0.6508217 0.6549901 0.6582507 0.6608042 0.6629207 0.6649003
[8] 0.6668472 0.6687443 0.6705665 0.6723035 0.6739539 0.6755194 0.6770028
[15] 0.6784075 0.6797370 0.6809951 0.6821853 0.6833114 0.6843770 0.6853854
[22] 0.6863398 0.6872434 0.6880990 0.6889093 0.6896769 0.6904043 0.6910936
[29] 0.6917470 0.6923664 0.6929539 0.6935110 0.6940395 0.6945410 0.6950169
[36] 0.6954685 0.6958972 0.6963042 0.6966907 0.6970577 0.6974063 0.6977374
[43] 0.6980519 0.6983508 0.6986348 0.6989047 0.6991612 0.6994050 0.6996367
[50] 0.6998571 0.7000666 0.7002657 0.7004552 0.7006353 0.7008066 0.7009696
[57] 0.7011245 0.7012720 0.7014122 0.7015457 0.7016726 0.7017934 0.7019083
[64] 0.7020177 0.7021217 0.7022208 0.7023150 0.7024047 0.7024901 0.7025713
[71] 0.7026487 0.7027223 0.7027924 0.7028591 0.7029226 0.7029830 0.7030405
[78] 0.7030953 0.7031475 0.7031971 0.7032444 0.7032894 0.7033322 0.7033730
[85] 0.7034119 0.7034489 0.7034841 0.7035176 0.7035496 0.7035800 0.7036089
[92] 0.7036365 0.7036627 0.7036877 0.7037115 0.7037342 0.7037558 0.7037764
[99] 0.7037959 0.7038146 0.7038323 0.7038493 0.7038654 0.7038807 0.7038953
[106] 0.7039092 0.7039225 0.7039351 0.7039471 0.7039585 0.7039694 0.7039798
[113] 0.7039897 0.7039991 0.7040081 0.7040166 0.7040247 0.7040325 0.7040399
[120] 0.7040469 0.7040536 0.7040600 0.7040660 0.7040718 0.7040773 0.7040826
[127] 0.7040876 0.7040923 0.7040968 0.7041012 0.7041053 0.7041092 0.7041129
[134] 0.7041165 0.7041199 0.7041231 0.7041261 0.7041291 0.7041319 0.7041345
[141] 0.7041370 0.7041394 0.7041417 0.7041439 0.7041460 0.7041480 0.7041499
[148] 0.7041516 0.7041534 0.7041550 0.7041565 0.7041580 0.7041594 0.7041608
[155] 0.7041620 0.7041633 0.7041644 0.7041655 0.7041666 0.7041676 0.7041685
[162] 0.7041694 0.7041703 0.7041711 0.7041719 0.7041727 0.7041734 0.7041740
[169] 0.7041747 0.7041753 0.7041759 0.7041765 0.7041770 0.7041775 0.7041780
[176] 0.7041784 0.7041789 0.7041793 0.7041797 0.7041801 0.7041804 0.7041808
[183] 0.7041811 0.7041814 0.7041817 0.7041820 0.7041822 0.7041825 0.7041827
[190] 0.7041830 0.7041832 0.7041834 0.7041836 0.7041838 0.7041840 0.7041842
[197] 0.7041843 0.7041845 0.7041846 0.7041848 0.7041849 0.7041850 0.7041852
[204] 0.7041853 0.7041854 0.7041855 0.7041856 0.7041857 0.7041858 0.7041859
[211] 0.7041860 0.7041860 0.7041861 0.7041862 0.7041863 0.7041863 0.7041864
[218] 0.7041864 0.7041865 0.7041866 0.7041866 0.7041867 0.7041867 0.7041867
[225] 0.7041868 0.7041868 0.7041869 0.7041869 0.7041869 0.7041870 0.7041870
[232] 0.7041870 0.7041871 0.7041871 0.7041871 0.7041871 0.7041872 0.7041872
[239] 0.7041872 0.7041872 0.7041872 0.7041873 0.7041873 0.7041873 0.7041873
[246] 0.7041873 0.7041873 0.7041874 0.7041874 0.7041874 0.7041874 0.7041874
[253] 0.7041874 0.7041874 0.7041874 0.7041875 0.7041875 0.7041875 0.7041875
[260] 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875
[267] 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875 0.7041876 0.7041876
[274] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
[281] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
[288] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
[295] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
For u1
u1
[1] 105.37122 104.28497 103.19437 102.19782 101.34808 100.69007 100.21667 99.88967 99.66755
[10] 99.51631 99.41138 99.33623 99.28022 99.23661 99.20121 99.17139 99.14549 99.12247
[19] 99.10163 99.08255 99.06490 99.04849 99.03315 99.01877 99.00527 98.99257 98.98060
[28] 98.96932 98.95867 98.94862 98.93912 98.93015 98.92166 98.91364 98.90605 98.89886
[37] 98.89206 98.88562 98.87952 98.87374 98.86826 98.86307 98.85815 98.85348 98.84905
[46] 98.84485 98.84087 98.83709 98.83350 98.83009 98.82686 98.82379 98.82087 98.81810
[55] 98.81547 98.81297 98.81059 98.80833 98.80619 98.80415 98.80221 98.80037 98.79861
[64] 98.79695 98.79536 98.79386 98.79243 98.79106 98.78977 98.78853 98.78736 98.78624
[73] 98.78518 98.78417 98.78321 98.78230 98.78143 98.78060 98.77981 98.77906 98.77835
[82] 98.77767 98.77702 98.77640 98.77582 98.77526 98.77473 98.77422 98.77374 98.77329
[91] 98.77285 98.77243 98.77204 98.77166 98.77130 98.77096 98.77064 98.77033 98.77003
[100] 98.76975 98.76949 98.76923 98.76899 98.76876 98.76854 98.76833 98.76813 98.76794
[109] 98.76776 98.76759 98.76743 98.76727 98.76712 98.76698 98.76685 98.76672 98.76660
[118] 98.76648 98.76637 98.76626 98.76616 98.76607 98.76598 98.76589 98.76581 98.76573
[127] 98.76565 98.76558 98.76551 98.76545 98.76539 98.76533 98.76527 98.76522 98.76517
[136] 98.76512 98.76507 98.76503 98.76499 98.76495 98.76491 98.76487 98.76484 98.76481
[145] 98.76478 98.76475 98.76472 98.76469 98.76467 98.76464 98.76462 98.76460 98.76457
[154] 98.76455 98.76454 98.76452 98.76450 98.76448 98.76447 98.76445 98.76444 98.76442
[163] 98.76441 98.76440 98.76439 98.76438 98.76437 98.76436 98.76435 98.76434 98.76433
[172] 98.76432 98.76431 98.76430 98.76430 98.76429 98.76428 98.76428 98.76427 98.76427
[181] 98.76426 98.76425 98.76425 98.76425 98.76424 98.76424 98.76423 98.76423 98.76423
[190] 98.76422 98.76422 98.76422 98.76421 98.76421 98.76421 98.76420 98.76420 98.76420
[199] 98.76420 98.76419 98.76419 98.76419 98.76419 98.76419 98.76419 98.76418 98.76418
[208] 98.76418 98.76418 98.76418 98.76418 98.76418 98.76417 98.76417 98.76417 98.76417
[217] 98.76417 98.76417 98.76417 98.76417 98.76417 98.76417 98.76417 98.76417 98.76416
[226] 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416
[235] 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416
[244] 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416
[253] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[262] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[271] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[280] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[289] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[298] 98.76415 98.76415 98.76415 98.76415
for u2
[1] 133.5728 133.8861 134.2721 134.6356 134.9464 135.1737 135.3096 135.3706 135.3799 135.3572
[11] 135.3157 135.2642 135.2078 135.1499 135.0923 135.0362 134.9820 134.9302 134.8809 134.8340
[21] 134.7895 134.7473 134.7073 134.6695 134.6337 134.5997 134.5676 134.5371 134.5083 134.4809
[31] 134.4550 134.4305 134.4072 134.3851 134.3641 134.3442 134.3254 134.3075 134.2905 134.2743
[41] 134.2590 134.2445 134.2307 134.2175 134.2051 134.1932 134.1820 134.1713 134.1611 134.1515
[51] 134.1423 134.1335 134.1252 134.1173 134.1098 134.1027 134.0959 134.0895 134.0833 134.0775
[61] 134.0719 134.0666 134.0616 134.0568 134.0523 134.0479 134.0438 134.0399 134.0361 134.0326
[71] 134.0292 134.0260 134.0229 134.0200 134.0172 134.0146 134.0121 134.0097 134.0074 134.0052
[81] 134.0032 134.0012 133.9993 133.9975 133.9958 133.9942 133.9927 133.9912 133.9898 133.9885
[91] 133.9872 133.9860 133.9849 133.9838 133.9827 133.9818 133.9808 133.9799 133.9791 133.9782
[101] 133.9775 133.9767 133.9760 133.9754 133.9747 133.9741 133.9735 133.9730 133.9725 133.9720
[111] 133.9715 133.9710 133.9706 133.9702 133.9698 133.9694 133.9691 133.9687 133.9684 133.9681
[121] 133.9678 133.9675 133.9673 133.9670 133.9668 133.9665 133.9663 133.9661 133.9659 133.9657
[131] 133.9655 133.9654 133.9652 133.9651 133.9649 133.9648 133.9646 133.9645 133.9644 133.9643
[141] 133.9642 133.9640 133.9639 133.9639 133.9638 133.9637 133.9636 133.9635 133.9634 133.9634
[151] 133.9633 133.9632 133.9632 133.9631 133.9631 133.9630 133.9630 133.9629 133.9629 133.9628
[161] 133.9628 133.9627 133.9627 133.9627 133.9626 133.9626 133.9626 133.9625 133.9625 133.9625
[171] 133.9625 133.9624 133.9624 133.9624 133.9624 133.9623 133.9623 133.9623 133.9623 133.9623
[181] 133.9623 133.9622 133.9622 133.9622 133.9622 133.9622 133.9622 133.9622 133.9622 133.9621
[191] 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621
[201] 133.9621 133.9621 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[211] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[221] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[231] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[241] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[251] 133.9620 133.9620 133.9620 133.9620 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[261] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[271] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[281] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[291] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[301] 133.9619
For sigma1 square:
[1] 220.12489 205.10096 183.53226 160.65836 141.18629 127.45956 118.93847 113.86190 110.77411
[10] 108.80379 107.47407 106.52342 105.80421 105.23069 104.75194 104.33723 103.96770 103.63162
[19] 103.32155 103.03264 102.76167 102.50639 102.26517 102.03679 101.82027 101.61481 101.41971
[28] 101.23438 101.05826 100.89085 100.73171 100.58039 100.43649 100.29964 100.16948 100.04567
[37] 99.92790 99.81586 99.70927 99.60785 99.51136 99.41954 99.33217 99.24902 99.16990
[46] 99.09459 99.02292 98.95471 98.88979 98.82799 98.76917 98.71318 98.65988 98.60914
[55] 98.56084 98.51486 98.47108 98.42941 98.38973 98.35196 98.31599 98.28174 98.24914
[64] 98.21810 98.18854 98.16039 98.13359 98.10807 98.08377 98.06063 98.03860 98.01762
[73] 97.99764 97.97861 97.96049 97.94324 97.92681 97.91116 97.89626 97.88207 97.86855
[82] 97.85568 97.84342 97.83175 97.82063 97.81005 97.79996 97.79036 97.78122 97.77251
[91] 97.76421 97.75631 97.74879 97.74162 97.73479 97.72829 97.72210 97.71621 97.71059
[100] 97.70524 97.70015 97.69530 97.69067 97.68627 97.68208 97.67809 97.67429 97.67067
[109] 97.66722 97.66393 97.66080 97.65782 97.65498 97.65228 97.64970 97.64725 97.64491
[118] 97.64269 97.64057 97.63855 97.63663 97.63480 97.63305 97.63139 97.62981 97.62830
[127] 97.62687 97.62550 97.62420 97.62296 97.62178 97.62065 97.61958 97.61856 97.61759
[136] 97.61666 97.61578 97.61494 97.61414 97.61338 97.61265 97.61196 97.61130 97.61067
[145] 97.61008 97.60951 97.60897 97.60845 97.60796 97.60749 97.60704 97.60662 97.60621
[154] 97.60583 97.60546 97.60511 97.60478 97.60446 97.60416 97.60387 97.60360 97.60334
[163] 97.60309 97.60285 97.60263 97.60241 97.60221 97.60201 97.60183 97.60165 97.60148
[172] 97.60132 97.60117 97.60102 97.60088 97.60075 97.60062 97.60051 97.60039 97.60028
[181] 97.60018 97.60008 97.59999 97.59990 97.59981 97.59973 97.59965 97.59958 97.59951
[190] 97.59944 97.59938 97.59932 97.59926 97.59921 97.59915 97.59910 97.59906 97.59901
[199] 97.59897 97.59893 97.59889 97.59885 97.59881 97.59878 97.59875 97.59872 97.59869
[208] 97.59866 97.59863 97.59861 97.59859 97.59856 97.59854 97.59852 97.59850 97.59848
[217] 97.59846 97.59845 97.59843 97.59841 97.59840 97.59839 97.59837 97.59836 97.59835
[226] 97.59834 97.59832 97.59831 97.59830 97.59829 97.59829 97.59828 97.59827 97.59826
[235] 97.59825 97.59825 97.59824 97.59823 97.59823 97.59822 97.59822 97.59821 97.59821
[244] 97.59820 97.59820 97.59819 97.59819 97.59818 97.59818 97.59818 97.59817 97.59817
[253] 97.59817 97.59816 97.59816 97.59816 97.59816 97.59815 97.59815 97.59815 97.59815
[262] 97.59814 97.59814 97.59814 97.59814 97.59814 97.59814 97.59813 97.59813 97.59813
[271] 97.59813 97.59813 97.59813 97.59813 97.59813 97.59812 97.59812 97.59812 97.59812
[280] 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812
[289] 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811
[298] 97.59811 97.59811 97.59811 97.59811
For sigma2 square
[1] 559.5878 525.6849 505.7973 488.0545 472.0863 458.8586 449.1209 442.7654 439.1009 437.3237
[11] 436.7687 436.9631 437.5961 438.4720 439.4702 440.5184 441.5732 442.6096 443.6137 444.5780
[21] 445.4991 446.3760 447.2092 447.9998 448.7495 449.4602 450.1336 450.7719 451.3767 451.9501
[31] 452.4935 453.0088 453.4975 453.9609 454.4006 454.8177 455.2135 455.5891 455.9457 456.2843
[41] 456.6057 456.9110 457.2010 457.4764 457.7380 457.9866 458.2229 458.4474 458.6608 458.8636
[51] 459.0564 459.2397 459.4140 459.5797 459.7373 459.8872 460.0297 460.1653 460.2943 460.4170
[61] 460.5337 460.6447 460.7503 460.8509 460.9465 461.0375 461.1241 461.2065 461.2850 461.3596
[71] 461.4307 461.4983 461.5627 461.6240 461.6823 461.7378 461.7907 461.8410 461.8889 461.9345
[81] 461.9779 462.0192 462.0586 462.0960 462.1317 462.1657 462.1980 462.2288 462.2581 462.2861
[91] 462.3126 462.3380 462.3621 462.3850 462.4069 462.4277 462.4475 462.4664 462.4844 462.5015
[101] 462.5178 462.5333 462.5481 462.5622 462.5756 462.5883 462.6005 462.6121 462.6231 462.6336
[111] 462.6436 462.6532 462.6622 462.6709 462.6791 462.6869 462.6944 462.7015 462.7083 462.7147
[121] 462.7209 462.7267 462.7323 462.7376 462.7427 462.7475 462.7521 462.7564 462.7606 462.7646
[131] 462.7683 462.7719 462.7754 462.7786 462.7817 462.7847 462.7875 462.7902 462.7927 462.7952
[141] 462.7975 462.7997 462.8018 462.8038 462.8057 462.8075 462.8093 462.8109 462.8125 462.8140
[151] 462.8154 462.8167 462.8180 462.8193 462.8204 462.8216 462.8226 462.8236 462.8246 462.8255
[161] 462.8264 462.8272 462.8280 462.8288 462.8295 462.8302 462.8308 462.8315 462.8321 462.8326
[171] 462.8332 462.8337 462.8342 462.8346 462.8351 462.8355 462.8359 462.8363 462.8366 462.8370
[181] 462.8373 462.8376 462.8379 462.8382 462.8385 462.8387 462.8390 462.8392 462.8394 462.8397
[191] 462.8399 462.8401 462.8402 462.8404 462.8406 462.8407 462.8409 462.8410 462.8412 462.8413
[201] 462.8414 462.8416 462.8417 462.8418 462.8419 462.8420 462.8421 462.8422 462.8422 462.8423
[211] 462.8424 462.8425 462.8425 462.8426 462.8427 462.8427 462.8428 462.8428 462.8429 462.8429
[221] 462.8430 462.8430 462.8431 462.8431 462.8432 462.8432 462.8432 462.8433 462.8433 462.8433
[231] 462.8434 462.8434 462.8434 462.8434 462.8435 462.8435 462.8435 462.8435 462.8435 462.8436
[241] 462.8436 462.8436 462.8436 462.8436 462.8436 462.8437 462.8437 462.8437 462.8437 462.8437
[251] 462.8437 462.8437 462.8437 462.8437 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438
[261] 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438
[271] 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439
[281] 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439
[291] 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439
[301] 462.8439
library(car)
x<-c(119.0,96.0,146.2,138.6,143.4,98.2,124.5,114.1,136.2,136.4,
184.8,79.8,151.9,114.2,145.7,95.9,97.3,136.4,109.2,103.2)
densityPlot(x)
p_0<-0.6
u1_0<-105
u2_0<-130
sigma1_0<-15
sigma2_0<-25
p<-c()
pi<-c()
u1<-c()
u2<-c()
sigma1_2<-c()
sigma2_2<-c()
s<-c()
s1<-c()
diff<-c()
j<-1 #this is imporant
s<-c(p_0,u1_0,u2_0,sigma1_0^2,sigma2_0^2) #initial guess of p,u1,u2,sigma1, sigma2
p_i_0<-p_0*dnorm(x,u2_0,sigma2_0)/((1-p_0)*dnorm(x,u1_0,sigma1_0)+p_0*dnorm(x,u2_0,sigma2_0))
p[j]<-mean(p_i_0)
u1[j]<-sum((1-p_i_0)*x)/sum(1-p_i_0)
u2[j]<-sum(p_i_0*x)/sum(p_i_0)
sigma1_2[j]<-sum((1-p_i_0)*(x-u1_0)^2)/sum(1-p_i_0)
sigma2_2[j]<-sum(p_i_0*(x-u2_0)^2)/sum(p_i_0)
s1<-c(p[j],u1[j],u2[j],sigma1_2[j],sigma2_2[j])
for(i in 1:5){
diff[i]<-abs(s1[i]-s[i])
}
for(i in 1:5){ #in fact we don't need this, we can mainly focus on p
while(diff[i]>0.000001){
s<-c(p[j],u1[j],u2[j],sigma1_2[j],sigma2_2[j])
p_i<-p[j]*dnorm(x,u2[j],(sigma2_2[j])^0.5)/((1-p[j])*dnorm(x,u1[j],sigma1_2[j]^0.5)+p[j]*dnorm(x,u2[j],sigma2_2[j]^0.5))
#p_i will be updated by p,u1,u2,sigma1 and sigma2
u1[j+1]<-sum((1-p_i)*x)/sum(1-p_i)
u2[j+1]<-sum(p_i*x)/sum(p_i)
sigma1_2[j+1]<-sum((1-p_i)*(x-u1[j+1])^2)/sum(1-p_i)
sigma2_2[j+1]<-sum(p_i*(x-u2[j+1])^2)/sum(p_i)
p[j+1]<-mean(p_i)
s1<-c(p[j+1],u1[j+1],u2[j+1],sigma1_2[j+1],sigma2_2[j+1])
diff[i]<-abs(s1[i]-s[i])
j=j+1
}
}
#results:
After 301 iterations all parameters are within 0.00000 accuracy
For p:
[1] 0.6446007 0.6508217 0.6549901 0.6582507 0.6608042 0.6629207 0.6649003
[8] 0.6668472 0.6687443 0.6705665 0.6723035 0.6739539 0.6755194 0.6770028
[15] 0.6784075 0.6797370 0.6809951 0.6821853 0.6833114 0.6843770 0.6853854
[22] 0.6863398 0.6872434 0.6880990 0.6889093 0.6896769 0.6904043 0.6910936
[29] 0.6917470 0.6923664 0.6929539 0.6935110 0.6940395 0.6945410 0.6950169
[36] 0.6954685 0.6958972 0.6963042 0.6966907 0.6970577 0.6974063 0.6977374
[43] 0.6980519 0.6983508 0.6986348 0.6989047 0.6991612 0.6994050 0.6996367
[50] 0.6998571 0.7000666 0.7002657 0.7004552 0.7006353 0.7008066 0.7009696
[57] 0.7011245 0.7012720 0.7014122 0.7015457 0.7016726 0.7017934 0.7019083
[64] 0.7020177 0.7021217 0.7022208 0.7023150 0.7024047 0.7024901 0.7025713
[71] 0.7026487 0.7027223 0.7027924 0.7028591 0.7029226 0.7029830 0.7030405
[78] 0.7030953 0.7031475 0.7031971 0.7032444 0.7032894 0.7033322 0.7033730
[85] 0.7034119 0.7034489 0.7034841 0.7035176 0.7035496 0.7035800 0.7036089
[92] 0.7036365 0.7036627 0.7036877 0.7037115 0.7037342 0.7037558 0.7037764
[99] 0.7037959 0.7038146 0.7038323 0.7038493 0.7038654 0.7038807 0.7038953
[106] 0.7039092 0.7039225 0.7039351 0.7039471 0.7039585 0.7039694 0.7039798
[113] 0.7039897 0.7039991 0.7040081 0.7040166 0.7040247 0.7040325 0.7040399
[120] 0.7040469 0.7040536 0.7040600 0.7040660 0.7040718 0.7040773 0.7040826
[127] 0.7040876 0.7040923 0.7040968 0.7041012 0.7041053 0.7041092 0.7041129
[134] 0.7041165 0.7041199 0.7041231 0.7041261 0.7041291 0.7041319 0.7041345
[141] 0.7041370 0.7041394 0.7041417 0.7041439 0.7041460 0.7041480 0.7041499
[148] 0.7041516 0.7041534 0.7041550 0.7041565 0.7041580 0.7041594 0.7041608
[155] 0.7041620 0.7041633 0.7041644 0.7041655 0.7041666 0.7041676 0.7041685
[162] 0.7041694 0.7041703 0.7041711 0.7041719 0.7041727 0.7041734 0.7041740
[169] 0.7041747 0.7041753 0.7041759 0.7041765 0.7041770 0.7041775 0.7041780
[176] 0.7041784 0.7041789 0.7041793 0.7041797 0.7041801 0.7041804 0.7041808
[183] 0.7041811 0.7041814 0.7041817 0.7041820 0.7041822 0.7041825 0.7041827
[190] 0.7041830 0.7041832 0.7041834 0.7041836 0.7041838 0.7041840 0.7041842
[197] 0.7041843 0.7041845 0.7041846 0.7041848 0.7041849 0.7041850 0.7041852
[204] 0.7041853 0.7041854 0.7041855 0.7041856 0.7041857 0.7041858 0.7041859
[211] 0.7041860 0.7041860 0.7041861 0.7041862 0.7041863 0.7041863 0.7041864
[218] 0.7041864 0.7041865 0.7041866 0.7041866 0.7041867 0.7041867 0.7041867
[225] 0.7041868 0.7041868 0.7041869 0.7041869 0.7041869 0.7041870 0.7041870
[232] 0.7041870 0.7041871 0.7041871 0.7041871 0.7041871 0.7041872 0.7041872
[239] 0.7041872 0.7041872 0.7041872 0.7041873 0.7041873 0.7041873 0.7041873
[246] 0.7041873 0.7041873 0.7041874 0.7041874 0.7041874 0.7041874 0.7041874
[253] 0.7041874 0.7041874 0.7041874 0.7041875 0.7041875 0.7041875 0.7041875
[260] 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875
[267] 0.7041875 0.7041875 0.7041875 0.7041875 0.7041875 0.7041876 0.7041876
[274] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
[281] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
[288] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
[295] 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876 0.7041876
For u1
u1
[1] 105.37122 104.28497 103.19437 102.19782 101.34808 100.69007 100.21667 99.88967 99.66755
[10] 99.51631 99.41138 99.33623 99.28022 99.23661 99.20121 99.17139 99.14549 99.12247
[19] 99.10163 99.08255 99.06490 99.04849 99.03315 99.01877 99.00527 98.99257 98.98060
[28] 98.96932 98.95867 98.94862 98.93912 98.93015 98.92166 98.91364 98.90605 98.89886
[37] 98.89206 98.88562 98.87952 98.87374 98.86826 98.86307 98.85815 98.85348 98.84905
[46] 98.84485 98.84087 98.83709 98.83350 98.83009 98.82686 98.82379 98.82087 98.81810
[55] 98.81547 98.81297 98.81059 98.80833 98.80619 98.80415 98.80221 98.80037 98.79861
[64] 98.79695 98.79536 98.79386 98.79243 98.79106 98.78977 98.78853 98.78736 98.78624
[73] 98.78518 98.78417 98.78321 98.78230 98.78143 98.78060 98.77981 98.77906 98.77835
[82] 98.77767 98.77702 98.77640 98.77582 98.77526 98.77473 98.77422 98.77374 98.77329
[91] 98.77285 98.77243 98.77204 98.77166 98.77130 98.77096 98.77064 98.77033 98.77003
[100] 98.76975 98.76949 98.76923 98.76899 98.76876 98.76854 98.76833 98.76813 98.76794
[109] 98.76776 98.76759 98.76743 98.76727 98.76712 98.76698 98.76685 98.76672 98.76660
[118] 98.76648 98.76637 98.76626 98.76616 98.76607 98.76598 98.76589 98.76581 98.76573
[127] 98.76565 98.76558 98.76551 98.76545 98.76539 98.76533 98.76527 98.76522 98.76517
[136] 98.76512 98.76507 98.76503 98.76499 98.76495 98.76491 98.76487 98.76484 98.76481
[145] 98.76478 98.76475 98.76472 98.76469 98.76467 98.76464 98.76462 98.76460 98.76457
[154] 98.76455 98.76454 98.76452 98.76450 98.76448 98.76447 98.76445 98.76444 98.76442
[163] 98.76441 98.76440 98.76439 98.76438 98.76437 98.76436 98.76435 98.76434 98.76433
[172] 98.76432 98.76431 98.76430 98.76430 98.76429 98.76428 98.76428 98.76427 98.76427
[181] 98.76426 98.76425 98.76425 98.76425 98.76424 98.76424 98.76423 98.76423 98.76423
[190] 98.76422 98.76422 98.76422 98.76421 98.76421 98.76421 98.76420 98.76420 98.76420
[199] 98.76420 98.76419 98.76419 98.76419 98.76419 98.76419 98.76419 98.76418 98.76418
[208] 98.76418 98.76418 98.76418 98.76418 98.76418 98.76417 98.76417 98.76417 98.76417
[217] 98.76417 98.76417 98.76417 98.76417 98.76417 98.76417 98.76417 98.76417 98.76416
[226] 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416
[235] 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416
[244] 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416 98.76416
[253] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[262] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[271] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[280] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[289] 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415 98.76415
[298] 98.76415 98.76415 98.76415 98.76415
for u2
[1] 133.5728 133.8861 134.2721 134.6356 134.9464 135.1737 135.3096 135.3706 135.3799 135.3572
[11] 135.3157 135.2642 135.2078 135.1499 135.0923 135.0362 134.9820 134.9302 134.8809 134.8340
[21] 134.7895 134.7473 134.7073 134.6695 134.6337 134.5997 134.5676 134.5371 134.5083 134.4809
[31] 134.4550 134.4305 134.4072 134.3851 134.3641 134.3442 134.3254 134.3075 134.2905 134.2743
[41] 134.2590 134.2445 134.2307 134.2175 134.2051 134.1932 134.1820 134.1713 134.1611 134.1515
[51] 134.1423 134.1335 134.1252 134.1173 134.1098 134.1027 134.0959 134.0895 134.0833 134.0775
[61] 134.0719 134.0666 134.0616 134.0568 134.0523 134.0479 134.0438 134.0399 134.0361 134.0326
[71] 134.0292 134.0260 134.0229 134.0200 134.0172 134.0146 134.0121 134.0097 134.0074 134.0052
[81] 134.0032 134.0012 133.9993 133.9975 133.9958 133.9942 133.9927 133.9912 133.9898 133.9885
[91] 133.9872 133.9860 133.9849 133.9838 133.9827 133.9818 133.9808 133.9799 133.9791 133.9782
[101] 133.9775 133.9767 133.9760 133.9754 133.9747 133.9741 133.9735 133.9730 133.9725 133.9720
[111] 133.9715 133.9710 133.9706 133.9702 133.9698 133.9694 133.9691 133.9687 133.9684 133.9681
[121] 133.9678 133.9675 133.9673 133.9670 133.9668 133.9665 133.9663 133.9661 133.9659 133.9657
[131] 133.9655 133.9654 133.9652 133.9651 133.9649 133.9648 133.9646 133.9645 133.9644 133.9643
[141] 133.9642 133.9640 133.9639 133.9639 133.9638 133.9637 133.9636 133.9635 133.9634 133.9634
[151] 133.9633 133.9632 133.9632 133.9631 133.9631 133.9630 133.9630 133.9629 133.9629 133.9628
[161] 133.9628 133.9627 133.9627 133.9627 133.9626 133.9626 133.9626 133.9625 133.9625 133.9625
[171] 133.9625 133.9624 133.9624 133.9624 133.9624 133.9623 133.9623 133.9623 133.9623 133.9623
[181] 133.9623 133.9622 133.9622 133.9622 133.9622 133.9622 133.9622 133.9622 133.9622 133.9621
[191] 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621 133.9621
[201] 133.9621 133.9621 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[211] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[221] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[231] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[241] 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620 133.9620
[251] 133.9620 133.9620 133.9620 133.9620 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[261] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[271] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[281] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[291] 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619 133.9619
[301] 133.9619
For sigma1 square:
[1] 220.12489 205.10096 183.53226 160.65836 141.18629 127.45956 118.93847 113.86190 110.77411
[10] 108.80379 107.47407 106.52342 105.80421 105.23069 104.75194 104.33723 103.96770 103.63162
[19] 103.32155 103.03264 102.76167 102.50639 102.26517 102.03679 101.82027 101.61481 101.41971
[28] 101.23438 101.05826 100.89085 100.73171 100.58039 100.43649 100.29964 100.16948 100.04567
[37] 99.92790 99.81586 99.70927 99.60785 99.51136 99.41954 99.33217 99.24902 99.16990
[46] 99.09459 99.02292 98.95471 98.88979 98.82799 98.76917 98.71318 98.65988 98.60914
[55] 98.56084 98.51486 98.47108 98.42941 98.38973 98.35196 98.31599 98.28174 98.24914
[64] 98.21810 98.18854 98.16039 98.13359 98.10807 98.08377 98.06063 98.03860 98.01762
[73] 97.99764 97.97861 97.96049 97.94324 97.92681 97.91116 97.89626 97.88207 97.86855
[82] 97.85568 97.84342 97.83175 97.82063 97.81005 97.79996 97.79036 97.78122 97.77251
[91] 97.76421 97.75631 97.74879 97.74162 97.73479 97.72829 97.72210 97.71621 97.71059
[100] 97.70524 97.70015 97.69530 97.69067 97.68627 97.68208 97.67809 97.67429 97.67067
[109] 97.66722 97.66393 97.66080 97.65782 97.65498 97.65228 97.64970 97.64725 97.64491
[118] 97.64269 97.64057 97.63855 97.63663 97.63480 97.63305 97.63139 97.62981 97.62830
[127] 97.62687 97.62550 97.62420 97.62296 97.62178 97.62065 97.61958 97.61856 97.61759
[136] 97.61666 97.61578 97.61494 97.61414 97.61338 97.61265 97.61196 97.61130 97.61067
[145] 97.61008 97.60951 97.60897 97.60845 97.60796 97.60749 97.60704 97.60662 97.60621
[154] 97.60583 97.60546 97.60511 97.60478 97.60446 97.60416 97.60387 97.60360 97.60334
[163] 97.60309 97.60285 97.60263 97.60241 97.60221 97.60201 97.60183 97.60165 97.60148
[172] 97.60132 97.60117 97.60102 97.60088 97.60075 97.60062 97.60051 97.60039 97.60028
[181] 97.60018 97.60008 97.59999 97.59990 97.59981 97.59973 97.59965 97.59958 97.59951
[190] 97.59944 97.59938 97.59932 97.59926 97.59921 97.59915 97.59910 97.59906 97.59901
[199] 97.59897 97.59893 97.59889 97.59885 97.59881 97.59878 97.59875 97.59872 97.59869
[208] 97.59866 97.59863 97.59861 97.59859 97.59856 97.59854 97.59852 97.59850 97.59848
[217] 97.59846 97.59845 97.59843 97.59841 97.59840 97.59839 97.59837 97.59836 97.59835
[226] 97.59834 97.59832 97.59831 97.59830 97.59829 97.59829 97.59828 97.59827 97.59826
[235] 97.59825 97.59825 97.59824 97.59823 97.59823 97.59822 97.59822 97.59821 97.59821
[244] 97.59820 97.59820 97.59819 97.59819 97.59818 97.59818 97.59818 97.59817 97.59817
[253] 97.59817 97.59816 97.59816 97.59816 97.59816 97.59815 97.59815 97.59815 97.59815
[262] 97.59814 97.59814 97.59814 97.59814 97.59814 97.59814 97.59813 97.59813 97.59813
[271] 97.59813 97.59813 97.59813 97.59813 97.59813 97.59812 97.59812 97.59812 97.59812
[280] 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812 97.59812
[289] 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811 97.59811
[298] 97.59811 97.59811 97.59811 97.59811
For sigma2 square
[1] 559.5878 525.6849 505.7973 488.0545 472.0863 458.8586 449.1209 442.7654 439.1009 437.3237
[11] 436.7687 436.9631 437.5961 438.4720 439.4702 440.5184 441.5732 442.6096 443.6137 444.5780
[21] 445.4991 446.3760 447.2092 447.9998 448.7495 449.4602 450.1336 450.7719 451.3767 451.9501
[31] 452.4935 453.0088 453.4975 453.9609 454.4006 454.8177 455.2135 455.5891 455.9457 456.2843
[41] 456.6057 456.9110 457.2010 457.4764 457.7380 457.9866 458.2229 458.4474 458.6608 458.8636
[51] 459.0564 459.2397 459.4140 459.5797 459.7373 459.8872 460.0297 460.1653 460.2943 460.4170
[61] 460.5337 460.6447 460.7503 460.8509 460.9465 461.0375 461.1241 461.2065 461.2850 461.3596
[71] 461.4307 461.4983 461.5627 461.6240 461.6823 461.7378 461.7907 461.8410 461.8889 461.9345
[81] 461.9779 462.0192 462.0586 462.0960 462.1317 462.1657 462.1980 462.2288 462.2581 462.2861
[91] 462.3126 462.3380 462.3621 462.3850 462.4069 462.4277 462.4475 462.4664 462.4844 462.5015
[101] 462.5178 462.5333 462.5481 462.5622 462.5756 462.5883 462.6005 462.6121 462.6231 462.6336
[111] 462.6436 462.6532 462.6622 462.6709 462.6791 462.6869 462.6944 462.7015 462.7083 462.7147
[121] 462.7209 462.7267 462.7323 462.7376 462.7427 462.7475 462.7521 462.7564 462.7606 462.7646
[131] 462.7683 462.7719 462.7754 462.7786 462.7817 462.7847 462.7875 462.7902 462.7927 462.7952
[141] 462.7975 462.7997 462.8018 462.8038 462.8057 462.8075 462.8093 462.8109 462.8125 462.8140
[151] 462.8154 462.8167 462.8180 462.8193 462.8204 462.8216 462.8226 462.8236 462.8246 462.8255
[161] 462.8264 462.8272 462.8280 462.8288 462.8295 462.8302 462.8308 462.8315 462.8321 462.8326
[171] 462.8332 462.8337 462.8342 462.8346 462.8351 462.8355 462.8359 462.8363 462.8366 462.8370
[181] 462.8373 462.8376 462.8379 462.8382 462.8385 462.8387 462.8390 462.8392 462.8394 462.8397
[191] 462.8399 462.8401 462.8402 462.8404 462.8406 462.8407 462.8409 462.8410 462.8412 462.8413
[201] 462.8414 462.8416 462.8417 462.8418 462.8419 462.8420 462.8421 462.8422 462.8422 462.8423
[211] 462.8424 462.8425 462.8425 462.8426 462.8427 462.8427 462.8428 462.8428 462.8429 462.8429
[221] 462.8430 462.8430 462.8431 462.8431 462.8432 462.8432 462.8432 462.8433 462.8433 462.8433
[231] 462.8434 462.8434 462.8434 462.8434 462.8435 462.8435 462.8435 462.8435 462.8435 462.8436
[241] 462.8436 462.8436 462.8436 462.8436 462.8436 462.8437 462.8437 462.8437 462.8437 462.8437
[251] 462.8437 462.8437 462.8437 462.8437 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438
[261] 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438 462.8438
[271] 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439
[281] 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439
[291] 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439 462.8439
[301] 462.8439
2015年6月17日星期三
EM algorithm to impute missing value and underlying parameter
Genetic linkage data are from Rao, C. R. (1973), Linear Statistical Inference and Its Applications, 2nd Ed., New York: John Wiley & Sons. p368
x<-c(125,18,20,34)
n<-sum(x)
theta.0<-(x[1]-x[2]-x[3]+x[4])/n
theta.0
current_theta<-c()
new_theta<-c()
z11<-c()
z12<-c()
i<-1
current_theta[i]<-theta.0
new_theta[i]<-(x[1]*current_theta[i]+2*x[4]+x[4]*current_theta[i])/(n*current_theta[i]+2*(x[2]+x[3]+x[4]))
new_theta[i]
difference<-abs(new_theta[i]-current_theta[i])
difference
while(difference>0.00000001){
current_theta[i]<-new_theta[i]
new_theta[i+1]<-(x[1]*current_theta[i]+2*x[4]+x[4]*current_theta[i])/(n*current_theta[i]+2*(x[2]+x[3]+x[4]))
difference<-abs(new_theta[i+1]-current_theta[i])
z11[i]<-(0.5/(0.5+0.25*current_theta[i]))*x[1]
z12[i]<-((0.25*current_theta[i])/(0.5+0.25*current_theta[i]))*x[1]
i<-i+1
}
cbind(theta=current_theta,Z11=z11,Z12=z12)
Results: Z11 and Z12 are imputed missing values and thetas are mle estimate of parameter, 7 iterations will get 10^-8 accuracy.
theta Z11 Z12
[1,] 0.6251317 95.23332 29.76668
[2,] 0.6265968 95.18019 29.81981
[3,] 0.6267917 95.17314 29.82686
[4,] 0.6268175 95.17220 29.82780
[5,] 0.6268210 95.17207 29.82793
[6,] 0.6268214 95.17206 29.82794
[7,] 0.6268215 95.17206 29.82794
x<-c(125,18,20,34)
n<-sum(x)
theta.0<-(x[1]-x[2]-x[3]+x[4])/n
theta.0
current_theta<-c()
new_theta<-c()
z11<-c()
z12<-c()
i<-1
current_theta[i]<-theta.0
new_theta[i]<-(x[1]*current_theta[i]+2*x[4]+x[4]*current_theta[i])/(n*current_theta[i]+2*(x[2]+x[3]+x[4]))
new_theta[i]
difference<-abs(new_theta[i]-current_theta[i])
difference
while(difference>0.00000001){
current_theta[i]<-new_theta[i]
new_theta[i+1]<-(x[1]*current_theta[i]+2*x[4]+x[4]*current_theta[i])/(n*current_theta[i]+2*(x[2]+x[3]+x[4]))
difference<-abs(new_theta[i+1]-current_theta[i])
z11[i]<-(0.5/(0.5+0.25*current_theta[i]))*x[1]
z12[i]<-((0.25*current_theta[i])/(0.5+0.25*current_theta[i]))*x[1]
i<-i+1
}
cbind(theta=current_theta,Z11=z11,Z12=z12)
Results: Z11 and Z12 are imputed missing values and thetas are mle estimate of parameter, 7 iterations will get 10^-8 accuracy.
theta Z11 Z12
[1,] 0.6251317 95.23332 29.76668
[2,] 0.6265968 95.18019 29.81981
[3,] 0.6267917 95.17314 29.82686
[4,] 0.6268175 95.17220 29.82780
[5,] 0.6268210 95.17207 29.82793
[6,] 0.6268214 95.17206 29.82794
[7,] 0.6268215 95.17206 29.82794
2015年6月15日星期一
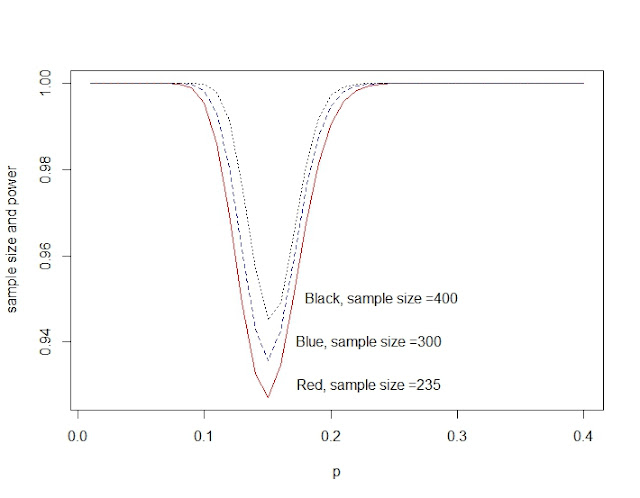
Power and sample size for Binomial distribution
power_n<-function(size){
p0<-51/235 #for calculate the critical region
c<-qbinom(p0,size, 1/6)
p<-seq(0.01,0.4,0.01)
pow<-1-dbinom(c,size,p)+dbinom(size-c,size,p) #the second part is very small can be omitted.
return(pow)
}
p<-seq(0.01,0.4,0.01)
plot(p,power_n(235),type="l",col="red")
lines(p,power_n(300),lty=2,col="blue")
lines(p,power_n(400),lty=3, col="black")
text(0.23,0.93,"Red, sample size =235")
text(0.23,0.94,"Blue, sample size =300")
text(0.24,0.95,"Black, sample size =400")
p0<-51/235 #for calculate the critical region
c<-qbinom(p0,size, 1/6)
p<-seq(0.01,0.4,0.01)
pow<-1-dbinom(c,size,p)+dbinom(size-c,size,p) #the second part is very small can be omitted.
return(pow)
}
p<-seq(0.01,0.4,0.01)
plot(p,power_n(235),type="l",col="red")
lines(p,power_n(300),lty=2,col="blue")
lines(p,power_n(400),lty=3, col="black")
text(0.23,0.93,"Red, sample size =235")
text(0.23,0.94,"Blue, sample size =300")
text(0.24,0.95,"Black, sample size =400")
2015年5月4日星期一
订阅:
评论 (Atom)